PAPUTRI (Trigonometric Rotating Board) as an innovation to enhance mathematics learning in trigonometry
Keywords:
Paputri Audio Visual Aids, Trigonometry, Math Learning MediaAbstract
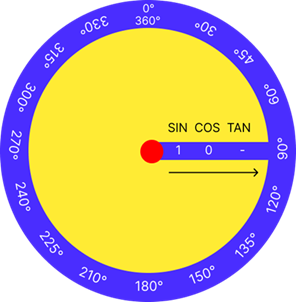
This study investigates the effectiveness of the Paputri (Trigonometric Rotating Board) audio-visual aid in enhancing the quality of mathematics learning, particularly in trigonometry. Employing a qualitative case study approach, the research involved third-semester students majoring in Mathematics Education at Universitas Negeri Malang, who acted as direct users of the teaching aid. The instruments used included the Paputri media, video recordings, and field notes. Data were collected through classroom observations and interactive analysis of video documentation and evaluation notes. The findings reveal that the integration of Paputri in trigonometry instruction effectively promotes students’ critical thinking, engagement, and conceptual understanding. Moreover, it fosters a more interactive and enjoyable learning environment that motivates students to actively participate in the learning process. These results highlight the pedagogical potential of manipulative and visual media in supporting mathematics learning. In conclusion, the use of Paputri as an audio-visual aid has a positive impact on students’ comprehension of trigonometric concepts. The study recommends that mathematics teachers incorporate similar innovative media in trigonometry teaching to enhance student engagement and enrich learning experiences.
Downloads
References
Barmby, P., Harries, T., Higgins, S., & Suggate, J. (2019). The array representation and primary children's understanding and reasoning in multiplication. Educational Studies in Mathematics, 100(3), 251-265. https://doi.org/10.1007/s10649-018-9860-1
Blackett, N., & Tall, D. (1991). Gender and the versatile learning of trigonometry using computer software. Educational Studies in Mathematics, 22(2), 149-175.
Brown, S. A. (2005). The trigonometric connection: Students' understanding of sine and cosine [Doctoral dissertation, Illinois State University].
Bruner, J. S. (1966). Toward a theory of instruction. Harvard University Press.
Carbonneau, K. J., & Marley, S. C. (2015). Instructional guidance and realism of manipulatives influence preschool children's mathematics learning. The Journal of Experimental Education, 83(4), 495-513. https://doi.org/10.1080/00220973.2014.989306
Carbonneau, K. J., Marley, S. C., & Selig, J. P. (2013). A meta-analysis of the efficacy of teaching mathematics with concrete manipulatives. Journal of Educational Psychology, 105(2), 380-400.
Clements, D. H. (1999). 'Concrete' manipulatives, concrete ideas. Contemporary Issues in Early Childhood, 1(1), 45-60.
Cohen, L., Manion, L., & Morrison, K. (2018). Research methods in education (8th ed.). Routledge. https://doi.org/10.4324/9781315456539
Creswell, J. W., & Creswell, J. D. (2018). Research design: Qualitative, quantitative, and mixed methods approaches (5th ed.). SAGE Publications.
Creswell, J. W., & Poth, C. N. (2018). Qualitative inquiry and research design: Choosing among five approaches (4th ed.). SAGE Publications.
Darmawan, P., & Yusuf, F. I. (2022). Analisis data kualitatif interaktif dalam penelitian pendidikan matematika. Jurnal Pendidikan Matematika Indonesia, 7(2), 45-56.
Demir, Ö. (2012). Students' concept development and understanding of sine and cosine functions. Educational Research and Reviews, 7(5), 103-110.
Dikovic, L. (2009). Implementing dynamic mathematics resources with GeoGebra at the college level. International Journal of Emerging Technologies in Learning, 4(3), 51-54.
Fajri, N., & Nida, I. (2019). Kesulitan siswa dalam memahami konsep trigonometri. Jurnal Pendidikan Matematika, 10(1), 78-89.
Febriani, R. (2022). Analisis kesulitan siswa dalam mempelajari trigonometri di sekolah menengah atas. Jurnal Inovasi Pendidikan Matematika, 4(2), 112-125.
Fi, C. (2003). Preservice secondary school mathematics teachers' knowledge of trigonometry: Subject matter knowledge, pedagogical content knowledge and envisioned pedagogy [Doctoral dissertation, University of Iowa].
Gür, H. (2009). Trigonometry learning. New Horizons in Education, 57(1), 67-80.
Güven, B., & Dede, Y. (2017). Examining social and sociomathematical norms in different classroom microcultures: Mathematics teacher education perspective. Educational Sciences: Theory & Practice, 17(1), 265-292. https://doi.org/10.12738/estp.2017.1.0298
Hannula, M. S. (2006). Motivation in mathematics: Goals reflected in emotions. Educational Studies in Mathematics, 63(2), 165-178.
Hasan, M., Milawati, T., Darodjat, D., Harahap, T. K., Tahrim, T., Anwari, A. M., Rahmat, A., Masdiana, M., & Indra, I. M. (2020). Media pembelajaran. Tahta Media Group.
Karunakaran, S. S., & Kim, H. J. (2020). University students' understanding of the sine function. International Journal of Mathematical Education in Science and Technology, 51(6), 889-910. https://doi.org/10.1080/0020739X.2019.1582891
Kolb, D. A. (1984). Experiential learning: Experience as the source of learning and development. Prentice Hall.
Lewin, K. M. (2015). Educational access, equity, and development: Planning to make rights realities. Fundamentals of Educational Planning, 98. UNESCO.
Lincoln, Y. S., & Guba, E. G. (1985). Naturalistic inquiry. SAGE Publications.
López, J., Robles, I., & Martín-Ramos, P. (2020). Learning mathematics with emerging methodologies—The escape room as a case study. Mathematics, 8(9), 1586. https://doi.org/10.3390/math8091586
Mendoza, M. C., & Camacho-Machín, M. (2021). Students' understanding of the concept of trigonometric ratios through the inverse problems. Eurasia Journal of Mathematics, Science and Technology Education, 17(2), em1940. https://doi.org/10.29333/ejmste/9682
Merriam, S. B., & Tisdell, E. J. (2016). Qualitative research: A guide to design and implementation (4th ed.). Jossey-Bass.
Miles, M. B., Huberman, A. M., & Saldaña, J. (2014). Qualitative data analysis: A methods sourcebook (3rd ed.). SAGE Publications.
Moore, K. C. (2014). Quantitative reasoning and the sine function: The case of Zac. Journal for Research in Mathematics Education, 45(1), 102-138.
Moyer, P. S. (2001). Are we having fun yet? How teachers use manipulatives to teach mathematics. Educational Studies in Mathematics, 47(2), 175-197.
National Council of Teachers of Mathematics. (2020). Catalyzing change in high school mathematics: Initiating critical conversations. NCTM.
National Research Council. (2001). Adding it up: Helping children learn mathematics. National Academy Press.
Nurahma, G. A., & Hendriani, W. (2021). Metode studi kasus dalam penelitian kualitatif. Jurnal Penelitian Psikologi, 12(3), 234-248.
Piaget, J. (1970). Science of education and the psychology of the child. Viking Press.
Powell, A. B., Francisco, J. M., & Maher, C. A. (2003). An analytical model for studying the development of learners' mathematical ideas and reasoning using videotape data. The Journal of Mathematical Behavior, 22(4), 405-435. https://doi.org/10.1016/j.jmathb.2003.09.002
Pratiwi, D. D., & Sari, D. S. (2020). The effectiveness of teaching aids in mathematics learning: A systematic review. Indonesian Journal of Mathematics Education, 3(1), 1-10.
Rau, M. A. (2017). Conditions for the effectiveness of multiple visual representations in enhancing STEM learning. Educational Psychology Review, 29(4), 717-761. https://doi.org/10.1007/s10648-016-9365-3
Ryan, R. M., & Deci, E. L. (2000). Self-determination theory and the facilitation of intrinsic motivation, social development, and well-being. American Psychologist, 55(1), 68-78.
Sowell, E. J. (1989). Effects of manipulative materials in mathematics instruction. Journal for Research in Mathematics Education, 20(5), 498-505.
Sweller, J. (1988). Cognitive load during problem solving: Effects on learning. Cognitive Science, 12(2), 257-285.
Thompson, P. W., Carlson, M. P., Byerley, C., & Hatfield, N. (2014). Schemes for thinking with magnitudes: A hypothesis about foundational reasoning abilities in algebra. In L. P. Steffe, K. C. Moore, & L. L. Hatfield (Eds.), Epistemic algebraic students: Emerging models of students' algebraic knowing (pp. 1-24). University of Wyoming.
Uribe-Flórez, L. J., & Wilkins, J. L. (2017). Manipulative use and elementary school students' mathematics learning. International Journal of Science and Mathematics Education, 15(8), 1541-1557. https://doi.org/10.1007/s10763-016-9757-0
Vygotsky, L. S. (1978). Mind in society: The development of higher psychological processes. Harvard University Press.
Weber, K. (2005). Students' understanding of trigonometric functions. Mathematics Education Research Journal, 17(3), 91-112.
Weber, K., Dawkins, P., & Mejía-Ramos, J. P. (2020). The relationship between mathematical practice and mathematics pedagogy in mathematics education research. ZDM Mathematics Education, 52(6), 1063-1074. https://doi.org/10.1007/s11858-020-01173-7
Yin, R. K. (2018). Case study research and applications: Design and methods (6th ed.). SAGE Publications.
Published
How to Cite
Issue
Section
Copyright (c) 2025 Aniisah Suhaa Salsabiila, Puguh Darmawan, Ronaldo Rafael Olivero-Acuña

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
PIJ is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
Articles in this journal are Open Access articles published under the Creative Commons CC BY-NC-SA License This license permits use, distribution and reproduction in any medium for non-commercial purposes only, provided the original work and source is properly cited. Any derivative of the original must be distributed under the same license as the original.







